IVM and the Octahedron-Tetrahedron Relationship
- Casey House

- Feb 17, 2023
- 3 min read
Updated: Nov 16
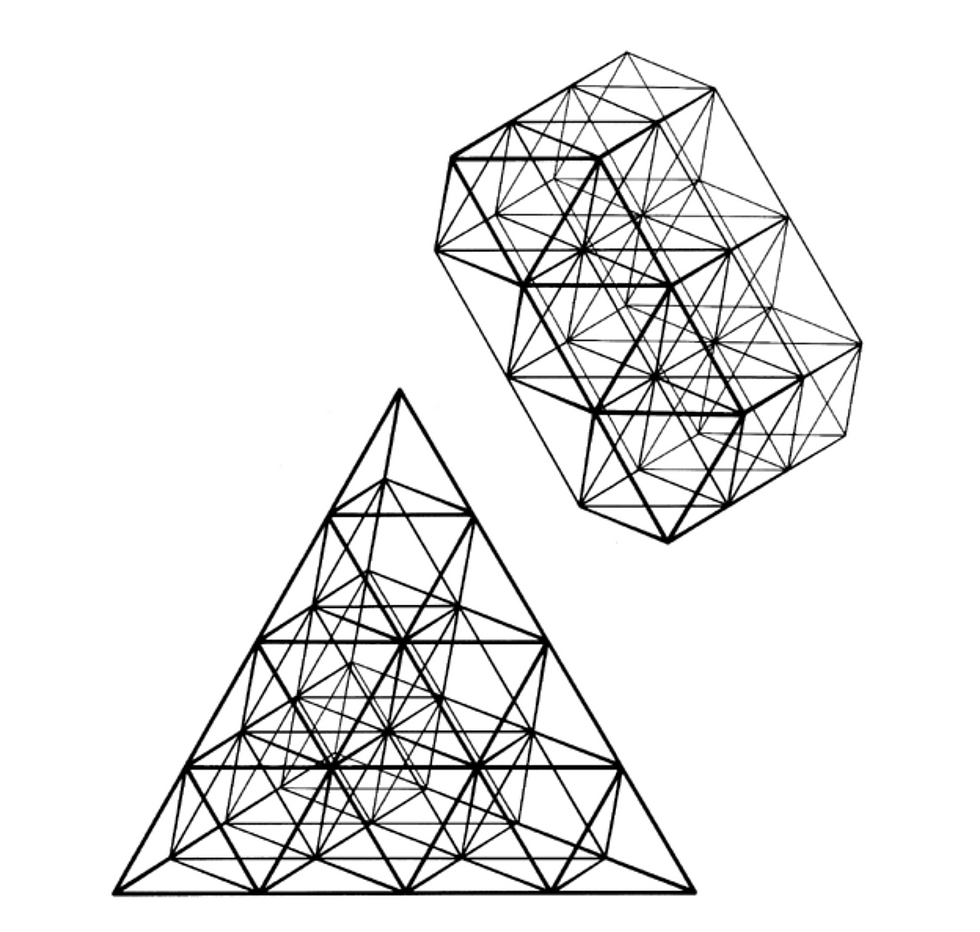
Synergetics Fig. 420.02 When the centers of equiradius spheres in closest packing are joined with lines, an isotropic vector matrix is formed. This constitutes an array of equilateral triangles which is seen as the comprehensive coordination frame of reference of nature's most economical, most comfortable structural interrelationships employing 60-degree association and disassociation. This provides an omnirational accounting system which, if arbitrarily accounted on a 90-degree basis, becomes inherently irrational. The isotropic vector matrix demonstrates the capability of accommodating all symmetrically and asymmetrically terminaled, high-frequency energy vectors of any structural shaping.
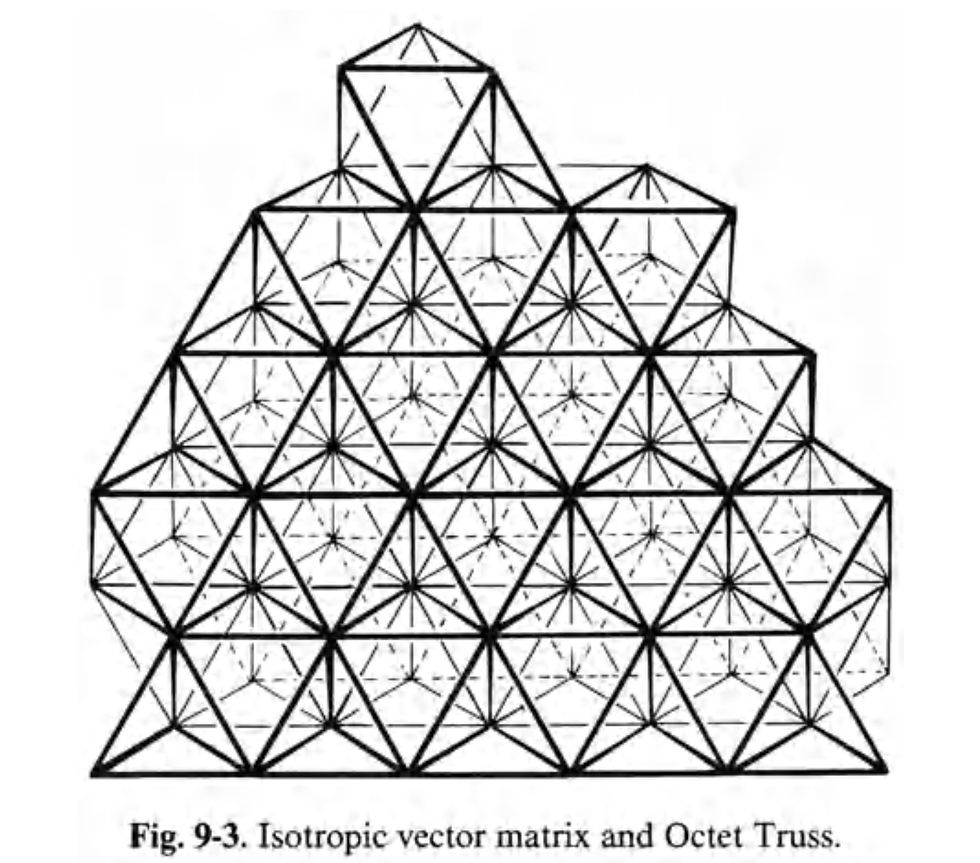
"It's not hard to see how Fuller's search for a geometry of vectors led him to the isotropic vector matrix. "Since vectors... produce conceptual structural models of energy events, and since my hypothetical generalization of Avogadro's law requires that 'all the conditions of energy be everywhere the same,''' ponders Fuller, "what does this condition look like as structured in vectorial geometry?" His answer is ready: "Obviously all the vectors must be the same length and all of them must interact [sic] at the same angles" The isotropic vector matrix, or IVM, takes the VE a step further, consisting of identical lengths and angles, not for vectors surround- ing just one point, but surrounding every point in an indefinite expanse. In Fuller's words, the IVM is "a multidimensional matrix in which the vertexes are everywhere the same and equidistant from one another" (222.25). It is not correct to conclude that the IVM consists of many vector equilibria packed together, for the VE by itself cannot fill space. To understand why not, we look at isolated sections of the IVM. As difficult as it is to visualize the overall matrix, a single row of alternating tetrahedra and octahedra, or even a planar expanse, can be easily envisioned. Separate planar layers are then stacked together in such a way that every octahedron is adjacent to a tetrahedron and vice versa. Every node in the IVM-as the origin of twelve unit vectors radiating outwardly-is the center of a local vector equilibrium. The ends of these unit vectors define the twelve vertices of the VE. ... However, this does not mean that adjacent cuboctahedra pack together to produce a space-filling expanse. A symmetrical array can be created by bringing the square faces of adjacent vector equilibria together, but they are necessarily separated by octahedral cavities-framed by the triangular faces of eight converging VEs. The unavoidable octahedra between adjacent VEs provide yet another manifestation of the specificity of the shape of space." - Amy Edmondson "A Fuller Explanation"
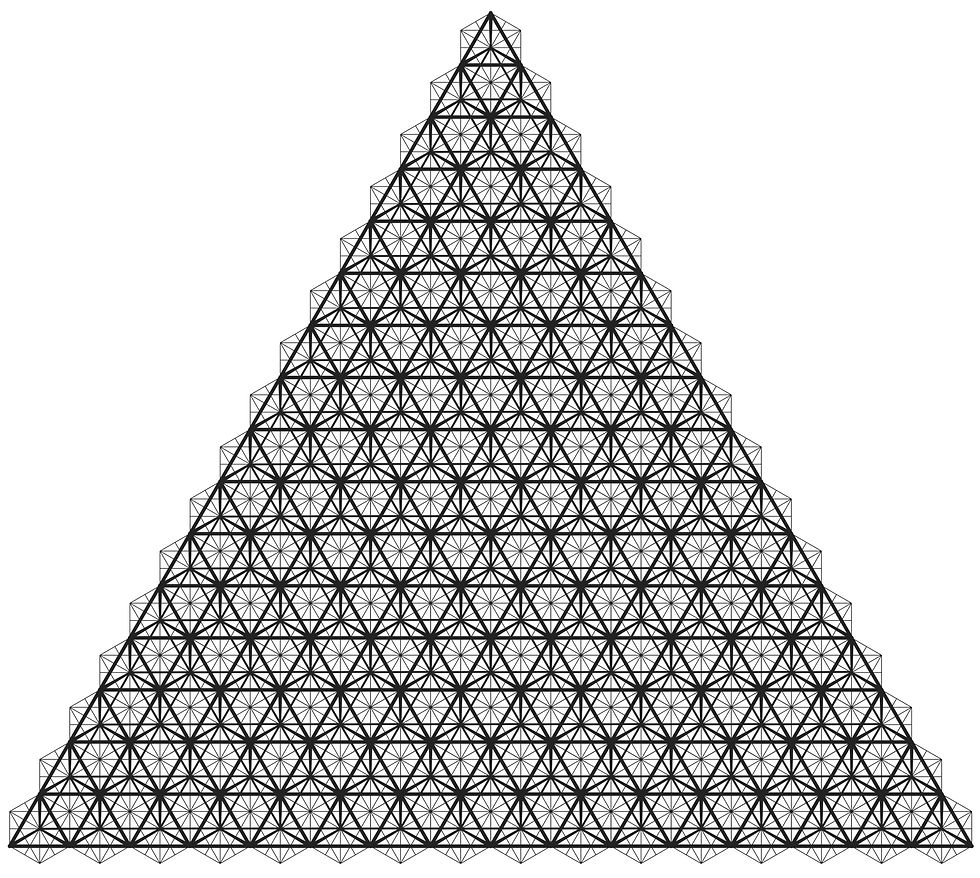
"The isotropic vector matrix gives us a description of the symmetry of space. We can think of this matrix as a framework of possible directions and configurations of ordered space, or more simply, as a frame of reference. It is a network of vectors specifically situated to model nature's eternal tendency toward equilibrium. Lines are forces, length is magnitude, and all is in balance. The IVM weaves together a number of synergetics ideas: minimum system of Universe, vector equilibrium (both exhibiting four planes of symmetry), twelve degrees of freedom, complementarity of octahedra and tetrahedra, space-filling, and stability (exclusively a product of triangulation). In so doing, it sets the stage for an energetic mathematics, and systematizes further investigation." -Amy Edmondson "A Fuller Explanation"




















Comments